Estudamos em postagens anteriores diversas relações e equações relacionadas aos triângulos. A seguir vamos aprender sobre alguns pontos notáveis em um triângulo, que estão presentes em todos eles e que possuem significados diferentes. Os pontos notáveis que estudaremos serão: O baricentro, o incentro, o ortocentro e o circuncentro. Para isso, vamos utilizar mais alguns conceitos de apoio, para melhor entendimento do assunto.
Para entender o conceito do baricentro, vamos considerar o seguinte triângulo:

Perceba que além dos vértices A, B e C, foram marcados também três pontos, que são os pontos médios de cada segmento. O ponto médio divide o seguimento exatamente ao meio. A mediana é um segmento de reta que liga o vértice oposto ao ponto médio de um segmento, ou seja, segmentos que fazem as ligações A-1, B-2 e C-3. O ponto em que se encontram as três mediatrizes do triângulo recebe o nome de baricentro. Observe a localização do baricentro no mesmo triângulo exemplo:

O baricentro, ponto em amarelo no triângulo acima, está posicionado no encontro das mediatrizes, e está representado pela letra B.
Vamos agora falar sobre o incentro do triângulo, e para isso vamos considerar o seguinte triângulo:

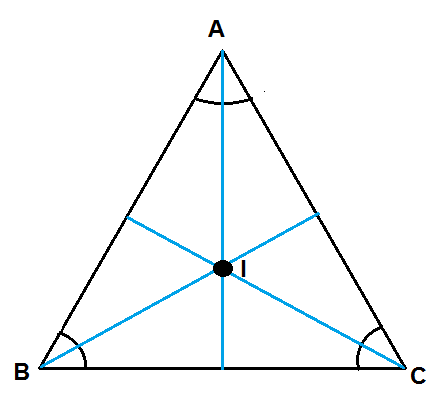
A bissetriz de um triângulo é definida como a reta que divide um de seus ângulos ao meio. Desta forma, a bissetriz do vértice A será um segmento de reta que particionará o seu ângulo ao meio, ligando até o lado oposto do triângulo. O Incentro é definido como o encontro das bissetrizes de um triângulo. Vamos posicionar as bissetrizes do triângulo acima, assim como o seu incentro:

Como mencionamos acima, o incentro (representado pela letra I) está localizado no ponto de intersecção entre as três bissetrizes do triângulo. Perceba que embora tenhamos utilizado triângulos diferentes para os exemplos, poderia ser utilizado um único triângulo! A escolha por diferentes modelos é feita para uma melhor visualização, mas os pontos que apresentamos nesta postagem valem para todos os triângulos, sendo inclusive um bom treino para se realizar ao final!
Vamos agora falar sobre o ortocentro, e para isso vamos utilizar o seguinte triângulo:

A altura de um triângulo é o segmento de reta que parte do vértice e faz um ângulo de 90 graus com o lado oposto do triângulo. O ortocentro é o ponto onde essas três alturas se cruzam, e assim como falamos, estará presente em todos os demais triângulos. O ortocentro está representado na figura abaixo:

Por fim, vamos definir o circuncentro de um triângulo. Para isso, precisamos entender o conceito de mediatriz. Observe o exemplo abaixo:

Você já deve ter notado que o triângulo é o mesmo do primeiro exemplo, e que novamente os pontos médios estão marcados, pois vamos utilizá-los novamente. A mediatriz é um segmento de reta que sai do ponto médio e é perpendicular ao seu vértice correspondente. Do encontro das três mediatrizes resulta o circuncentro do triângulo, ilustrado abaixo:

Com isso, estudamos sobre pontos importantes no interior de triângulos, e embora existam diversos pontos e definições, não será difícil compreendê-los através da realização de exercícios. Portanto pratique e não terá dificuldades com este assunto muito interessante!


1 comment