Veja Como Obter Valores Extremos de Uma Função Quadrática

Durante a análise de equações, é bastante comum precisarmos obter seu valor máximo ou mínimo, dependendo de sua aplicação. Para isso, utilizamos funções e recursos os quais permitem calcular rapidamente estes valores, permitindo resolver rapidamente os problemas deste tipo. Em nosso artigo de hoje, iremos apresentar a técnica do cálculo do vértice para as funções quadráticas.

Para uma função quadrática qualquer, do tipo ax² + bx + c = 0, que já apresentamos em nesta postagem, sabemos que a sua curva típica será uma parábola. Também já conhecemos a representação da mesma, observando que apresenta uma concavidade, a qual será importante no entendimento do assunto, visto que irá determinar se o valor extremo calculado é máximo ou mínimo da função.

A concavidade da parábola é determinada pelo termo que acompanha o valor quadrado da função, em nosso caso o termo a. Para valores de a positivos, temos que a função apresenta sua concavidade voltada para cima, e o valor que calcularemos será o valor mínimo da função. Caso o valor de a seja menor que zero, teremos uma função com concavidade virada para baixo, com um valor máximo para a função no ponto.

Agora que entendemos o significado do ponto em questão, vamos aprender a calculá-lo. Para isso, iremos utilizar o conceito de vértice da função quadrática. Para uma função quadrática qualquer, do mesmo tipo que utilizamos acima, o valor máximo da função será obtido no ponto Y_v, cujo valor será:

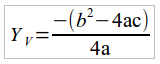
Devemos ressaltar que este valor obtido NÃO serve para indicar a concavidade da função. Este é um erro muito comum entre os alunos e, numa questão de múltipla escolha, irá desperdiçar todo o seu trabalho/tempo! Portanto, tome cuidado! A concavidade depende apenas do valor de a.

Também podemos obter o valor de X para o ponto anterior. Neste caso, X_v indicará a que distância da origem este valor irá ocorrer. O valor de X_v é obtido pela seguinte fórmula:

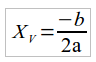
Por fim, percebemos que este é mais um conceito bem simples que aparece diversas vezes durante os exames. Ao dominá-lo você estará preparado para enfrentar as questões deste tipo durante o Enem. Adiante, vamos apresentar técnicas auxiliares para o cálculo dos valores extremos de uma função.

Até breve!