Como vimos em outro artigo aqui no infoEnem, a matriz quadrada é aquela que possui o mesmo número de linhas e de colunas (veja). Sendo assim, uma matriz do tipo a = nxm será uma matriz quadrada somente se n=m. No artigo de hoje, vamos definir alguns importantes conceitos, todos em relação a uma matriz quadrada.
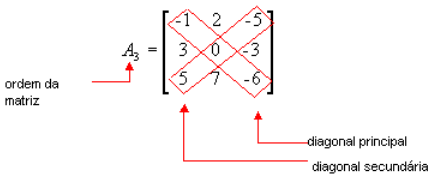
Partiremos então de um conceito bem simples, a ordem de uma matriz. A ordem de uma matriz quadrada é definida como o número de linhas (ou colunas) de sua matriz. Por exemplo, uma matriz de ordem três apresentará três linhas e três colunas. Para nossos próximos conceitos, usaremos uma matriz do tipo A = ixj com ordem n. A diagonal principal desta matriz corresponde a todos os termos tais que i = j. Já a diagonal secundária corresponde aos termos que, para uma matriz de ordem n apresentem a seguinte relação:
i+j = n+1
Embora possa parecer complicado na teoria, perceberemos que visualmente é de grande simplicidade identificar as diagonais de uma matriz, como em nosso exemplo a seguir:
Vamos agora registrar algumas variações da matriz quadrada e suas respectivas definições:
Indice
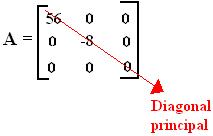
Matriz Diagonal
Uma matriz diagonal é aquela em que todos os elementos que não pertencem a diagonal principal são nulos.
Matriz Identidade
A matriz identidade pode ser definida como uma matriz que possui todos os elementos fora da diagonal principal nulos, enquanto todos os elementos da diagonal principal são iguais a 1. Em outras palavras, a matriz identidade se trata de uma matriz diagonal com todos os termos iguais a 1.
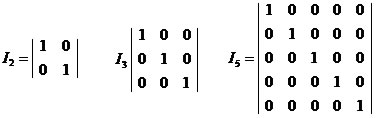
Matriz triangular superior
Uma matriz triangular superior apresenta todos os elementos abaixo de sua diagonal principal nulos, enquanto os elementos acima de sua diagonal podem assumir qualquer valor.
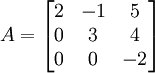
Matriz triangular inferior
Como já é esperado, a matriz triangular inferior apresenta os elementos acima de sua diagonal principal nulos, enquanto os outros podem assumir qualquer valor.
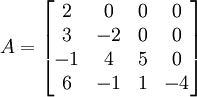
Enfim, estas são as variações possíveis para uma matriz quadrada. Em breve, daremos início ao estudo de operações que envolvam matrizes, tais como a soma e multiplicação.